| |
 |
Objetivos |
- Aprender a utilizar algunas de las funciones matemáticas más habituales en Gambas.
|
 |
Fuentes de información |
- http://www.gambas-es.org
- Libro “GAMBAS, programación visual con Software Libre”, de la
editorial EDIT LIN EDITORIAL S.L., cuyos autores son Daniel Campos
Fernández y José Luis Redrejo.
- Libro “Fundamentos de programación”, de la editorial Univ.
Politécnica de Valencia, cuyos autores son Mª Alpuente Fresnedo y otros.
|
 |
|
| |
1. Funciones matemáticas
Gambas dispone de una librería completa de funciones matemáticas
adicionales que nos permitirán realizar operaciones más allá de la suma,
resta, multiplicación y división. Entre dichas funciones tenemos: valor
absoluto, raíz cuadrada, signo de un número, logaritmo y operaciones
trigonométricas (seno, coseno, tangente, etc).
A continuación se muestran algunas funciones matemáticas:
Operación |
Descripción |
Abs (Número) |
Devuelve el valor absoluto de un número. |
Sqr (Número) |
Devuelve la raíz cuadrada de un número. |
Log (Número) |
Devuelve el logaritmo neperiano de un número. |
Log10 (Número) |
Devuelve el logaritmo en base 10 de un número. |
Sgn (Número) |
Devuelve el signo de un número. Si el número es 0, devuelve 0. Si es positivo, devuelve +1. Si es negativo, devuelve -1. |
La mejor forma de entender estas funciones es probando alguna de ellas en los programas.
- Abrimos Gambas.
- Hacemos clic en la opción Nuevo proyecto.
- Marcamos la opción Aplicación de consola y hacemos clic en el botón Siguiente.
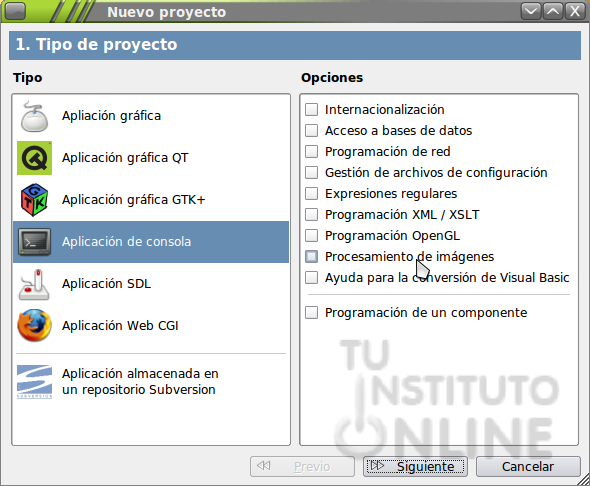
- Seleccionamos en nuestro directorio personal el directorio BASIC/1MTEXTO creado anteriormente Documentos/BASIC/1MTEXTO.
- Hacemos clic en el botón Siguiente.
- Le damos un nombre y título al proyecto. En el primer campo escribimos “16EcuacionGrado2”. En el segundo campo escribimos “Proyecto para obtener la solución de una ecuación de segundo grado”.
El asistente creará un nuevo directorio con el nombre del proyecto
(campo 1) y ahí irá introduciendo todos los archivos necesarios para el
desarrollo de la aplicación.
- Hacemos clic en OK.
|
 |
|
| |
- Ahora sin ayuda y aplicando todo lo que has aprendido hasta el momento deberás crear un programa para obtener las soluciones de una ecuación de segundo grado.
Sugerencias:
- Seguimos con el proyecto “16EcuacionGrado2”.
- Crea un nuevo módulo. Llámalo “SolEcuacion” y márcalo como Clase de inicio.
- Define 1 variable de tipo string para el número leído por teclado.
- Define 3 variables de tipo entero para a, b y c.
- Lee el número coeficiente de grado 2 (a) y conviértelo a entero.
- Leer el número coeficiente de grado 1 (b) y conviértelo a entero.
- Lee el término independiente (c) y conviértelo a entero.
- Efectúa la operación de la ecuación de 2º grado (primero la
parte positiva y luego la negativa, ya que el ordenador no admite el
operador ±):
- (-b - sqr(b^2 – 4ac))/2a
- (-b + sqr(b^2 – 4ac))/2a
- Muestra un mensaje de texto al usuario, indicando los resultados.
- Ejecuta el programa.
- Comprueba que el resultado es correcto. Prueba con varios números. Por ejemplo la ecuación x2-4x-1, donde a = 1, b = -4, c = -1.
- El resultado de la ejecución debe ser parecido a lo siguiente:
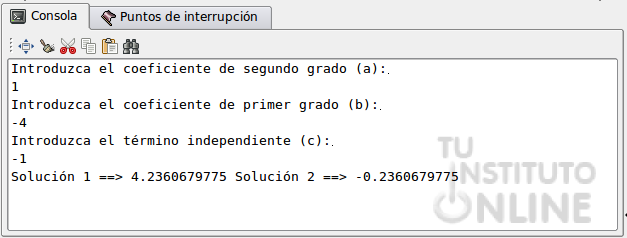
- Guarda los cambios en tu proyecto. No subas nada, ya lo subirás en el último ejercicio.
|
 |
|
| |
Ahora añadiremos un poco de control de errores al programa.
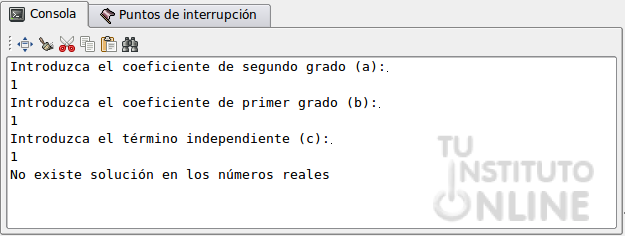
- Introduce los coeficientes de la ecuación de segundo grado x2+x+1, (es decir, a=1, b=1 y c=1)
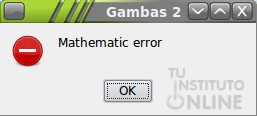
¿Qué ocurre?
Como podemos comprobar, 12-4*1*1 = -3, y al aplicar
la raíz cuadrada, Gambas nos da un error de ejecución. No existe la raíz
cuadrada de un número negativo, al menos en los números reales.
Vamos a solucionar el problema mediante la comprobación del valor del
determinante: si éste es negativo, la ecuación no tiene solución.
- Modifica el programa añadiendo la condición de comprobación.
Sugerencias:
- Añade una condición para comprobar si el determinante es
negativo. En caso afirmativo, muestra un mensaje y utilizar la
instrucción QUIT para salir del programa. En caso negativo, efectuar los
cálculos normalmente.
- Ejecuta el programa.
- Introduce los coeficientes de la ecuación de segundo grado x2+x+1.
- Comprueba que se muestra el mensaje de que no existe solución.
- Guarda los cambios en tu proyecto. No subas nada, ya lo subirás en el último ejercicio.
|
 |
|
| |
Ahora nos fijaremos en la optimización del programa.
El programa que hemos implementado funciona eficazmente, pero no es eficiente. Recordemos que EFICACIA ≠ EFICIENCIA:
- EFICACIA → Hacer las cosas correctas
- EFICIENCIA → Hacer las cosas correctamente
¿Por qué? Si nos fijamos, el determinante de la ecuación, es decir, (b^2 – 4ac), lo calculamos 3 veces.
Es lógico deducir que esto no es eficiente, puesto que cada vez que
realizamos una operación aritmética, el ordenador requiere de tiempo de
procesador y de memoria RAM para operar con las variables. Es por ello
que este programa podría ser 3 veces más rápido si calculamos el
determinante una sola vez.
De esta forma, nuestro programa es correcto (puesto que calcula
bien la solución) pero no es eficiente, ya que desperdicia los recursos
del ordenador. Al principio, es muy frecuente cometer este tipo de
“fallos”, puesto que la lógica del cerebro humano es distinta a la
lógica del computador.
Vamos a optimizar el programa:
- Modifica el programa para optimizar el cálculo del determinante.
Sugerencias:
- Crea una nueva variable y almacena el valor del determinante.
- Ejecutar el programa. Ahora mejor, ¿no?. En este programa no
se puede apreciar la diferencia, pero si estas instrucciones se
ejecutaran miles de veces, el coste temporal sería apreciable.
- Guarda los cambios en tu proyecto. No subas nada, ya lo subirás en el último ejercicio.
|
 |
|
| |
Ahora nos fijaremos de nuevo en las validaciones ante posibles errores del programa.
No hay mejor probador de un programa que alguien ajeno a su
programación. Después de haber implementado un módulo, ejecutarlo y
verificar que todo va bien, es frecuente sentirnos satisfechos.
Sin embargo, ¿qué pasaría si le decimos a nuestro mejor amigo
que lo pruebe? Seguro que encuentra algún defecto que se nos ha pasado
por alto.
Vamos a verificar mejor el programa:
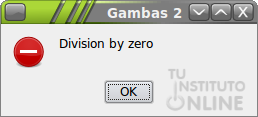
¿Qué ocurre si introducimos un 0 para el coeficiente de grado 2?
Al intentar dividir por cero, Gambas nos daría un error de cálculo que ya vimos en prácticas anteriores.
- Ejecuta el programa e introduce 0 para el coeficiente de
grado 2. En el mensaje que aparece, haz clic en el botón Stop. De este
modo, paramos el programa.
¿Cómo solucionar el problema?
Aplicamos la metodología “a problemas sencillos, soluciones
sencillas”. En este caso, bastará con comprobar que el coeficiente de
grado 2 no sea cero.
Sugerencias:
- Modifica el programa para comprobar el valor del
coeficiente de grado 2. Si es cero, muestra un mensaje de error y sal
del programa.
- Ejecutar el programa.
- Prueba a introducir un coeficiente de grado 2 con valor cero y comprueba que funciona correctamente.
- El resultado de la ejecución deber ser el siguiente:
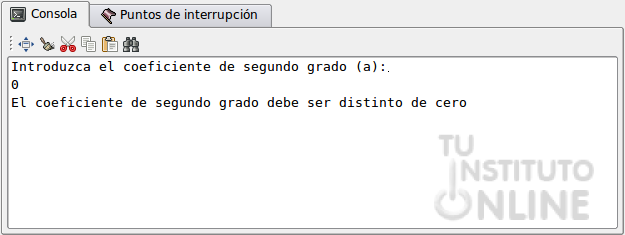
- Guarda los cambios en tu proyecto.
- Sube a la plataforma la captura de la pantalla donde
se vea la ejecución del programa que acabas de hacer con un 0 como
coeficiente de grado 2 y la mayor parte del código fuente que has
escrito.
- Sube también el fichero llamado SolEcuacion.module que podrás encontrar dentro de la carpeta del proyecto 16EcuacionGrado2.
|
|
|













